History of Mathematics in 50 Minutes
A very interesting lecture which is telling the story of some of the brightest minds in Mathematics and serving as a base for further research for the people that like the subject.
BBC Order And Disorder Episode 2 - Information
Professor Jim Al-Khalili investigates one of the most important concepts in the world today - information. He discovers how we harnessed the power of symbols, everything from the first alphabet to the electric telegraph through to the modern digital age. But on this journey he learns that information is not just about human communication, it is woven very profoundly into the fabric of reality.
Cantor's Infinities - Professor Raymond Flood
Although many people contributed to the study of infinity over the centuries it was Georg Cantor in the nineteenth century who established its modern development. Cantor created modern set theory and established the importance of one-to-one correspondence between sets. For example he showed that the set of all integers can be put into one-to-one correspondence with the set of all fractions and so these two sets have the same infinity. But he also proved the remarkable result that there are infinitely many infinities, all of different sizes.
Riemann's paradox: pi = infinity minus infinity
With the help of a very famous mathematician the Mathologer sets out to show how you can subtract infinity from infinity in a legit way to get exactly pi.
Math's Existential Crisis (Gödel's Incompleteness Theorems)
Math isn’t perfect, and math can prove it. In this video, we dive into Gödel’s incompleteness theorems, and what they mean for math.
Gödel's Incompleteness Theorem - Professor Tony Mann
A short mind-bending trip through the wonderful world of Mathematical Paradoxes: An examination of some recent work on paradoxes by the Austrian-American Mathematician Kurt Gödel. You can watch the full lecture by Professor Tony Mann here: http://www.gresham.ac.uk/lectures-and...
Beyond Computation: The P vs NP Problem - Michael Sipser
P vs NP is a problem in computer science and mathematics. It concerns the amount of time it takes to solve a problem on a computer. Some take a really long time. And we're not really sure why.
In a remarkable 1956 letter, the great logician Kurt Gödel asked the famous mathematician and computer pioneer John von Neumann whether certain computational problems could be solved without resorting to brute force search.
The Secret Life of Chaos - BBC
Chaos theory has a bad name, conjuring up images of unpredictable weather, economic crashes and science gone wrong. But there is a fascinating and hidden side to Chaos, one that scientists are only now beginning to understand.
It turns out that chaos theory answers a question that mankind has asked for millennia - how did we get here?
Chaos
For the people that are interested to know more on the subject.
Very good old Australian documentary about CHAOS theory
Chaos Theory - PBS
One of the best educational videos on Chaos Theory and Dynamic Systems that I have ever seen.
Chaos is order out of disorder, and order out of non-linearity.
When there is agreement within a system, the more complex a system, the better a bottom up/emergent organizational structure handles the diversity.
Fractals - Hunting the hidden dimensio
If you don't know what a fractal is or you want to learn more about fractals - this is the right movie to watch. After watching the movie, you may no more see the world (especially the nature, the processes, even the computer technology) as a random creation. If you like the mystery of the fractals, you may want find and read the "Fractal Time" by Gregg Braden, which I recommend.
Deepest Mandelbrot Set Zoom Animation ever - a New Record! 10^275 (2.1E275 or 2^915)
Cool and incredible: the result of a simple equation (below)!
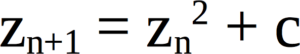
The Barber Paradox
Paradoxville has some weird rules regarding barbers. Will this barber find a way to shave himself or is this paradox foolproof?
Russell's Paradox (The Barber Paradox solved)
In this video, I show you the basics around Russell's Paradox and how to overcome it. Enjoy:)
The classic Liar's Paradox
When someone says "This sentence is false" or "I am a liar," just what does it mean? In this video, I describe the mathematical logic behind and 3 potential solutions to the classic Liar's Paradox.
Kurt Gödel's Philosophical Viewpoint
In his book, “A Logical Journey: from Gödel to Philosophy,” Hao Wang describes how he found a list of 14 philosophical points written by Gödel around the year 1960. Gödel had titled the list, “My Philosophical Viewpoint.” To understand Gödel's strange and magnificent worldview, we will go through each of these 14 points and analyze their greater significance.
The Secrets of Kurt Gödel
This is part 22 of 42. As you may have noticed, I am releasing them totally out of order, but that won't matter. In this part we begin our study of Kurt Gödel.
Secret History - Kurt Gödel and the Secrets of Genius
Continuing from the above one.
(1) Gödel, Self-Knowledge & Magic Mushrooms
What is Gödel's Incompleteness Theorem? What does it say about the limits of our understanding? Is rational thinking the most reliable path to knowledge? Do science, philosophy, maths or any other system of knowledge get us closer to absolute truth? Is self-reference, paradox and contradiction an inevitable part of our learning journey? And what on earth do Gödel's ideas have to do with self-growth, mysticism and magic mushrooms?
Gödel's Incompleteness Theorem places limits to what we can know, to the truths that can be established from within a given system. There will always be mystery at the edges of our understanding because our maps of the world will always be incomplete.
Any formal system of knowledge has self-reference built in it. From within the confines of the system, paradoxes and contradictions may arise; truths can only be established by transcending the system, by going beyond, by viewing the system from a wider perspective.
We can apply the ideas behind Gödel's Theorem to self-knowledge, to the age-old question "Who am I?". Where we place the boundaries of the self will determine the type of truths that we can establish about ourselves and the world. Self-growth can be seen as a journey of never-ending transcendence, of going beyond, by seeing reality with new eyes, from a new expanded frame of reference.
(2) Gödel, Self-Knowledge & Magic Mushrooms
What does the Perennial Philosophy have in common with Gödel's Incompleteness Theorem? Why is the science of mind so important? What is the mystic's path? How does the Self learn about itself? Is consciousness fundamental and - if so - why and how does it fragment itself?
This video explores:
- consciousness, self-knowledge & the nature of the mind
- wholeness and fragmentation of the Self
- mysticism, the Perennial Philosophy, transcendence and integration
- the Ego, its purpose and limitations
- spiritual and psychological approaches to expanding our sense of Self (our identity, our perspective)
- consciousness, self-awareness and self-reference
- Mind at Large; the brain as a filter metaphor. Henri Bergson
- Aldous Huxley, The Perennial Philosophy, The Doors of Perception
- Ken Wilber. Perennial Philosophy. Structures or levels of consciousness. Transpersonal psychology
- Bernardo Kastrup. Consciousness as the ground of all being. Consciousness filtering itself. The whirlpool metaphor. Self-localisation
- Huston Smith. The one-way mirror metaphor to explain the hierarchic levels of consciousness
- Rupert Spira. The science of mind. Ego not a mistake
- Carl Jung, Jungian psychology. Ego and Shadow. Transcendence and Integration (individuation)
- Ken Wilber. Transpersonal psychology, child development
- Symbolism: mother / child and altered states of consciousness. Subject / Object. I / You. Third person language
- Evolution of the self. Self-Knowledge. Fragmentation and wholeness
- Norman Friedman. The Self's journey. Self-knowledge, Incompleteness, Gödel, fragmentation of the self, transcendence. Infinite process; knowledge never complete














